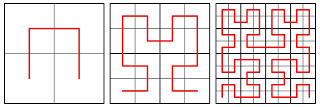
Recently, I returned to these dissections as methods for generating space-filling curves. For example, the Hilbert curve can be created by dissecting a square into four smaller squares, and connecting the centers:
In the first panel, the original square (thick black line) is dissected into four squares (thin black lines), whose centers are connected with the red curve. This process is repeated, wherein every square from the previous iteration is dissected into four smaller squares. The centers of all these new squares are connected with a line that is four copies of the previous curve, shrunken and rotated, and the result is a space-filling fractal curve.
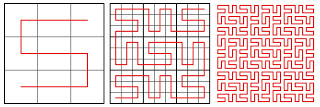
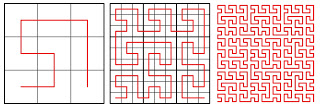
While the Hilbert curve is based on a 2 × 2 grid of four squares, other grids can be used. Here are the first three iterations of two curves based on 3 × 3 dissections of the square (in the third iteration, the squares have been left off for clarity):
The concept is quite general and can be extended to other shapes: develop a scheme for dissecting a base shape into smaller shapes and draw a curve connecting the centers. For practical reasons, I’ve kept my investigations to triangles and convex quadrilaterals (not necessarily rectangles). And for aesthetic reasons, I’ve decided that my curves will not cross themselves (the so-called “self-avoiding” curve). Here are three cases of dissecting a triangle into three smaller triangles. Note the appearance of shading, especially in the middle case.
Some very interesting opportunities arise when two different shapes are combined. For example, a quadrilateral can be broken up into triangles and quadrilaterals, each of which can be further decomposed into more triangles and quadrilaterals.
This technique has proven very fruitful for me and I’ll soon have more examples up on my website.