A few years ago, I played with fractions whose denominators are full reptend primes. The fractions have decimal expansions that repeat, as do most fractions. However, the repeating block for one fraction with a given denominator of this type is permutation of that for another fraction with the same denominator. For example, consider the denominator 7. The decimal expansions of its proper fractions are:
The same thing happens with other fractions whose denominators are full reptend primes. For example, 19 is a full reptend prime. When used as a denominator, its fractions repeat with a block of 18 digits. Here are some of them:
The comparisons need not be only with the first fraction’s block; any block can be compared with any other block (for the same denominator) to find out how many places it has been shifted, relative to the reference block. Let’s return to 7. In the table below, each row is for one of the six proper fractions with a denominator of 7. Each column is for the repeating block of one of the six fractions. The cells, then, give the place in the decimal expansion (row) where the particular repeating block (column) shows up. For example, the value in the cell for row 2/7 and column 1/7 is 5 (yellow highlight), meaning that 1/7’s repeating block (142857) appears beginning at the fifth place in 2/7’s decimal expansion. Likewise, the 3 in the cell intersecting the 5/7 row and the 3/7 column (orange highlight) means that 3/7’s repeating block (428571) begins at the third place in 5/7’s decimal expansion.
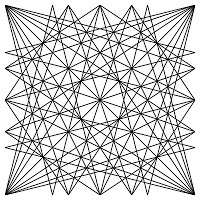
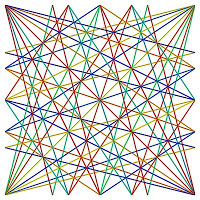
You may notice some patterns in the table. The diagonal from the top left to the bottom right is all 1s. This is because the reference fraction and the comparison block’s fraction are the same, so the comparison block always begins at the first place of its decimal expansion. Also, the other diagonal, from the bottom left to the upper right, is all 4s. In fact, all of the values in the table are arranged in diagonal bands, as this figure shows. Each colored line shows a band for the same values, with each value being represented by a different color. Extending the lines and removing the numbers and grid reveals the symmetry in the pattern.
- 1/7 = 0.142857142857142857142857142857…
- 2/7 = 0.285714285714285714285714285714…
- 3/7 = 0.428571428571428571428571428571…
- 4/7 = 0.571428571428571428571428571428…
- 5/7 = 0.714285714285714285714285714285…
- 6/7 = 0.857142857142857142857142857142…
The same thing happens with other fractions whose denominators are full reptend primes. For example, 19 is a full reptend prime. When used as a denominator, its fractions repeat with a block of 18 digits. Here are some of them:
- 1/19 = 0.05263157894736842105263157894737…
- 4/19 = 0.21052631578947368421052631578947…
- 9/19 = 0.47368421052631578947368421052632…
The comparisons need not be only with the first fraction’s block; any block can be compared with any other block (for the same denominator) to find out how many places it has been shifted, relative to the reference block. Let’s return to 7. In the table below, each row is for one of the six proper fractions with a denominator of 7. Each column is for the repeating block of one of the six fractions. The cells, then, give the place in the decimal expansion (row) where the particular repeating block (column) shows up. For example, the value in the cell for row 2/7 and column 1/7 is 5 (yellow highlight), meaning that 1/7’s repeating block (142857) appears beginning at the fifth place in 2/7’s decimal expansion. Likewise, the 3 in the cell intersecting the 5/7 row and the 3/7 column (orange highlight) means that 3/7’s repeating block (428571) begins at the third place in 5/7’s decimal expansion.
| Reference fraction | 1/7 142857 |
2/7 285714 |
3/7 428571 |
4/7 471428 |
5/7 714285 |
6/7 857142 |
|---|---|---|---|---|---|---|
| 1/7 = 0.142857… | 1 | 3 | 2 | 5 | 6 | 4 |
| 2/7 = 0.285714… | 5 | 1 | 6 | 3 | 4 | 2 |
| 3/7 = 0.428571… | 6 | 2 | 1 | 4 | 5 | 3 |
| 4/7 = 0.571428… | 3 | 5 | 4 | 1 | 2 | 6 |
| 5/7 = 0.714285… | 2 | 4 | 3 | 6 | 1 | 5 |
| 6/7 = 0.857142… | 4 | 6 | 5 | 2 | 3 | 1 |
You may notice some patterns in the table. The diagonal from the top left to the bottom right is all 1s. This is because the reference fraction and the comparison block’s fraction are the same, so the comparison block always begins at the first place of its decimal expansion. Also, the other diagonal, from the bottom left to the upper right, is all 4s. In fact, all of the values in the table are arranged in diagonal bands, as this figure shows. Each colored line shows a band for the same values, with each value being represented by a different color. Extending the lines and removing the numbers and grid reveals the symmetry in the pattern.
Larger full reptend prime denominators have similar, but more detailed, patterns. 19 has 18 different proper fractions, as opposed to six for a denominator of 7. Here is 19’s pattern, in black and white, to accentuate the structure, and in color to indicate the values.
The relatively sparse areas in the center and at the corners give a hint as to what happens with larger denominators. Here are the patterns for denominators of 61 and 193 (193’s is off-center to highlight the fractal detail).
Finally, here is an image for a denominator of 1019, which is about the limit of my current system.