High school math teacher Mike Aben gave this challenge to his algebra class:
It turns out that f(x) is a rational function, that is, the ratio of two polynomials. One way to see this is to realize that 1/(1/x) = x, so that by replacing “x” with “1/x” in the equation, a second equation would result. The two can then be solved simultaneously, yielding an equation for f(x).
This got me to thinking about how I might adapt this idea into a fractal equation. The x2 in the challenge equation is similar to the z2 + c in the Mandelbrot function, so I thought, let f(z) be such that 2f(z) – 3f(1/z) = z2 + c, and iterate f(z) to get a fractal. After a few seconds, I realized that I could generalize this to: let f(z) be such that Af(z) + Bf(1/z) = z2 + c. As in Mike’s challenge, the function is a rational one. When iterated, it can yield a wide variety of structures and images, depending on the values of A, B, and n.
Here is my challenge:
And here is the function to be iterated:
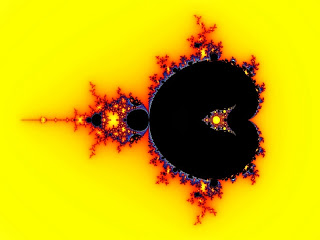
Here are a few examples. The first is a Mandelbrot set for 2f(z) - 4f(1/z) = z2 + c.
The colored regions in the centers of the main cardioid and the surrounding disks are reflective of this being a rational function and represent areas where z approaches 0.
Here is a zoom into the center, for 9f(z) - f(1/z) = z3+ c.
And, in closing, this image and the one at the top of the page are Julias for the quadratic form of this function.