Factoring polynomials is a standard part of most algebra curricula, but students often just see it as an exercise is symbol manipulation (as if that weren't enough!). However, some problems have geometric interpretations, which is what this image illustrates. Each of the 16 regions in the image (disregarding the white boards), has dimensions and an area that can be described in terms of variables, as listed in this table:
| Region | Row | Column | Color | Type | Width | Height | Area |
| 1 | 1 | 1 | blue | square | a | a | a2 |
| 2 | 1 | 2 | light gray | rectangle | b | a | a×b |
| 3 | 1 | 3 | light gray | rectangle | c | a | a×c |
| 4 | 1 | 4 | light gray | rectangle | d | a | a×d |
| 5 | 2 | 1 | light gray | rectangle | a | c | a×c |
| 6 | 2 | 2 | dark gray | rectangle | b | c | b×c |
| 7 | 2 | 3 | red | square | c | c | c2 |
| 8 | 2 | 4 | mid gray | rectangle | d | c | c×d |
| 9 | 3 | 1 | light gray | rectangle | a | b | a×b |
| 10 | 3 | 2 | yellow | square | b | b | b2 |
| 11 | 3 | 3 | dark gray | rectangle | c | b | b×c |
| 12 | 3 | 4 | mid gray | rectangle | d | b | b×d |
| 13 | 4 | 1 | light gray | rectangle | a | d | a×d |
| 14 | 4 | 2 | mid gray | rectangle | b | d | b×d |
| 15 | 4 | 3 | mid gray | rectangle | c | d | c×d |
| 16 | 4 | 4 | green | square | d | d | d2 |
For example, look at the square made up of the red square (region 7), the yellow square (region 10), and the two dark gray rectangles (regions 6 and 11). Combining the regions, the larger square has side lengths of b + c so its area is (b + c)2. The areas of the four pieces are c2, b2, b×c, and b×c. In terms of an equation:
(b + c)2 = b2 + c2 + 2bc .
The same analysis can be with the nine regions in the lower right corner of the image (red, yellow, and green squares, the two dark gray rectangles and the four mid gray rectangles). Comparing the areas of the nine-piece square (side length b + c + d) with the sum of the nine region areas yields:
(b + c + d)2 = b2 + c2+ d2 + 2bc + 2bd + 2cd.
Finally, all 16 regions in the image can be combining, giving a large square with side length a + b + c + d. Equating the total area with the sum of the parts gives the equation:
(a + b + c + d)2 = a2 + b2 + c2+ d2 + 2ab + 2ac + 2ad+ 2bc + 2bd + 2cd.
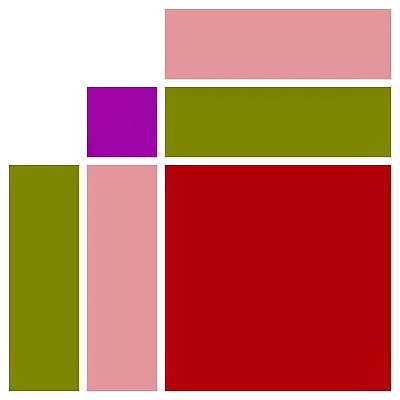
This image demonstrates the factoring of difference of squares:
x2 - y2 = (x + y)(x - y).
Let the larger square, made up of the red and purple square and the pink and gold rectangles, have a side length of x, so its area is x2. And the small purple square have a side length of y, so its area is y2. Then the area in the remaining three pieces (red square and pink and gold rectangles) is x2 - y2. Both rectangles have the same area, y × (x - y). So all three of these regions have the same area:
- the horizontal rectangle made up of the gold and pink vertical rectangles and the red square
- the vertical rectangle made up of the gold and pink horizontal rectangles and the red square
- the original square, less the small purple square (area of x2 - y2)
- (x - y)(x - y) + 2y(x - y), or
- (x - y + 2y)(x - y), or
- (x + y)(x - y)